As is well-known, in quantum mechanics the complex wave plays an essential role, which can explain the natural phenomena very well. In other words, it can be said that the rules of nature are written with logic using complex numbers. We are accustomed to the convenience of visualizing the overall behavior of a function by means of its graph. In the case of a complex function, however, this approach has not seemed workable for a long time because to depict a pair of complex numbers (an input z and the output of a function f ) we would need four dimensions.Especially in mathematical visualization, we have demonstrated thus far that how the fourth dimension is conceptualized seems to be successfully justified by using a cross section and a projection of an object appropriately, described in terms of polar coordinates (instead of Cartesian coordinates).
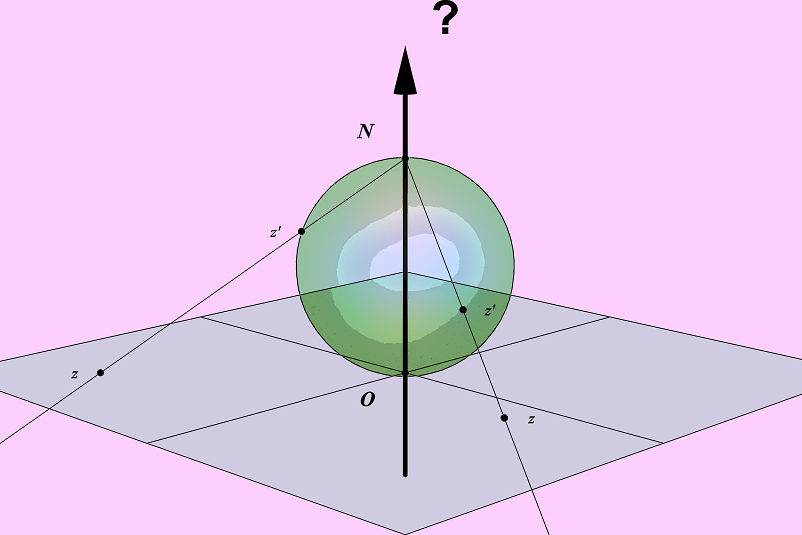
And we raise the question that has been neglected thus far: “What does the Riemann sphere’s axis stand for?” We show that the answer can be obtained only by observing from the inside the sphere by setting the viewpoint of the immersive environment on the point (0, 0), which is always undefined in projective geometry.




0 Comments