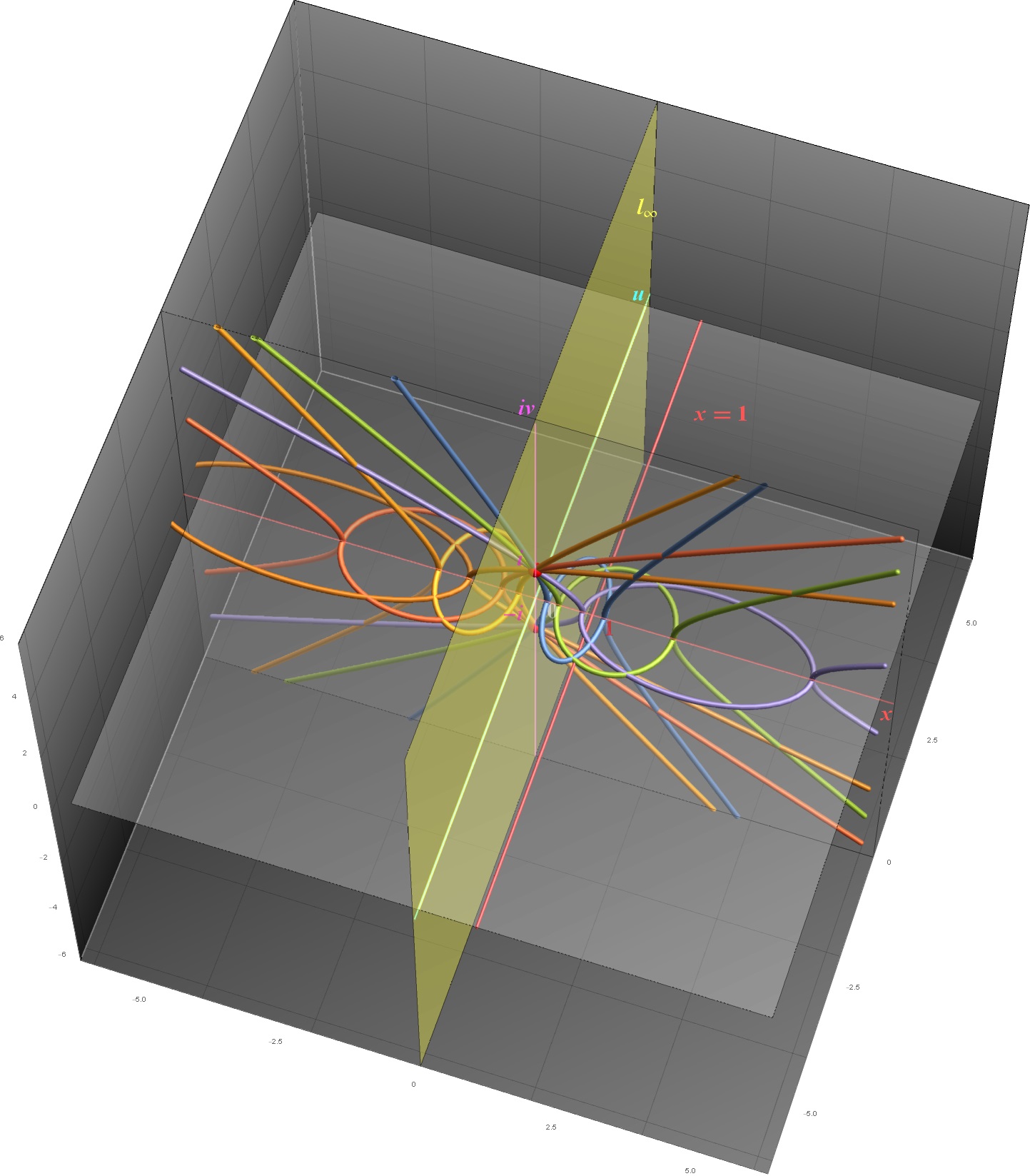
Abstract
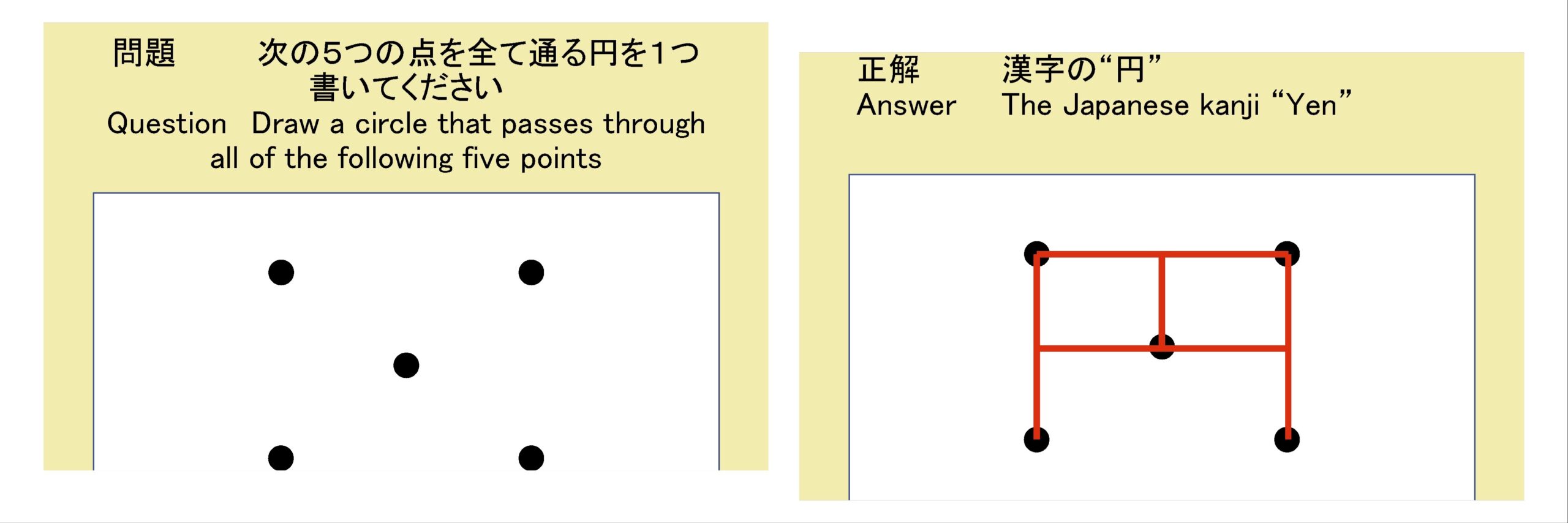
A question that gets students frequently in a TV program like the high school quiz bowl is “Draw a circle that passes through all of the following five points,” and the Japanese kanji Yen is supposed to be right. However, surprisingly enough, a mathematically sensible solution (notice not the punchline) exists for this problem.
The “five points” in that sentence sounds mathematically reasonable because the general quadratic equation that represents a conic section contains five undetermined coefficients;
x 2 + A x y + B y 2 + C x + D y + E = 0
It passes through five points (in a complex space, though) by its nature. Let these five points be, for example,
(0, 0), (1, ±1), (-1, ±√3 i )
By solving the simultaneous equations the answers are,
A = 0, B = 1, C = -2, D = 0, E = 0
we get the equation of the circle
(x – 1) 2 + y 2 = 1
And,… hey, wait a minute!
If so, a circle normally passes through 3 points (that are not on the same line determine a circle) in terms of the rule of plain common sense in junior high school mathematics, but when it passes through 5 points, where on earth are the remaining two?
We’ve come this far, we have to introduce a complex projective plane CP 2 = {(X, Y, Z ), x = X / Z, y = Y / Z | X, Y, Z ∈ C } instead of the ordinary Euclidean plane E 2 = {(x, y ) | x, y ∈ R }.
We can rewrite the equation of the circle using the projective coordinates (or homogeneous coordinates) as:
(X / Z ) 2 + (Y / Z ) 2 = 1 (that is, X 2 + Y 2 = Z 2)
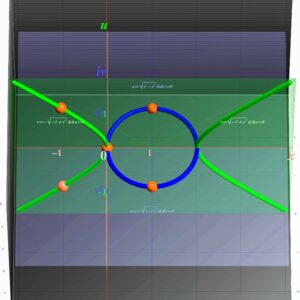
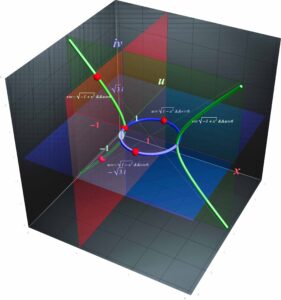
Now we can understand that all circles always pass through two “circular points at infinity (or isotropic points)” (1, ±i , 0) on the line at infinity Z = 0.
The concept of circular points at infinity was introduced by the French mathematician Jean-Victor Poncelet (1788-1867), who revived projective geometry. Believe it or not, they have never been correctly rendered so far, although many books on geometry have been introduced the points in the complex and infinitely distant territory.
The behavior of the circular points at infinity visualized for the first time in the world
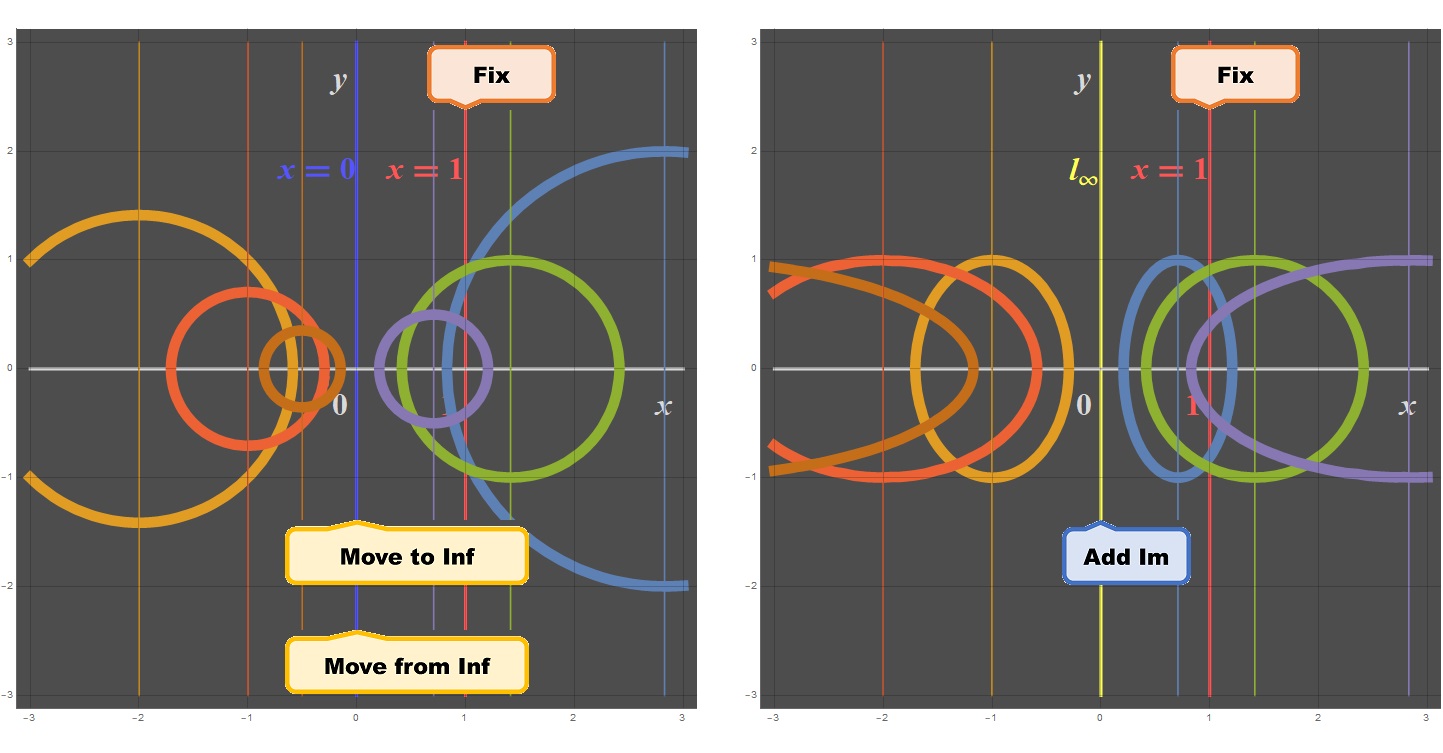
Locating two circular-points-at-infinity (red dots) by translating the line-at-infinity the u-axis (x = 0) while fixing the line x = 1 and then converting it (line-at-infinity) from real to complex.
We study an immersive virtual environment that allows the user to set environmental limits beyond three-dimensional Euclidean space E 3. More specifically, by setting the limits to n-dimensional complex projective space CP n, an element of both complex and infinitely distant domain can be naturally visualized as a recognizable form in the Euclidean 3-space. The problem here is that the higher the mathematics level, the more the visualization method tends to become abstract that only experts with advanced degrees can fathom. We’ll show how our figurative approach is essential for bridging the gap between elementary and more advanced mathematical visualizations.
Members
| Name | Affiliation | Web site |
|---|---|---|
 member |
Keio University | https://fj.ics.keio.ac.jp/ |
| aaa | aaa University | URL |
Video
ビデオがある場合は藤代研のYoutubeチャネルか何かにアップして、その動画をここに埋め込みましょう。こんな感じ↓
Publications
業績は新しい物から古いものの順番。ジャンルごとにordered list（ol要素）で管理し、リスト（li要素）にidを付与してください。olにはジャンルごとに以下のクラスを付与してください：論文誌->article、国際学会->internationalConf、国内会議->domesticConf、その他->others、資金->grant。li要素のidの命名は「プロジェクト名_publication_ジャンル名1」とします。
ジャンル名はジャーナル->article、国際学会->intconf、国内会議->domconf
業績をリンク（a要素）で囲って（DOIの部分は除いて）、業績ページへのリンクを貼ってください。その際a要素にはpublicationクラスを付与してください。DOIがある場合は必ず書いて、「https://doi.org/その論文のDOI」へのリンクを貼ること
ジャンルは必要に応じて増やしたり減らしたりしてください。書き方はTimeTubesXのページを参考にしてください。
Journals
- Author 1, Authort 2, Author 3: “title,” Journal Name, Vol. X, No. X, pp.XX–XXX, Date, Year [doi: DOI].
Conferences/Symposiums
International conferences/symposiums
Domestic conferences/symposiums
Presentations
Others
- 何かあれば
Grants
Grant-in-Aid for Scientific Research (A): 17H00737 (2017-)