概要
高校生クイズなどの鉄板ネタ?の一つに「次の5つの点を全て通る円を1つ書いてください」というのがあって、その答えは「漢字の“円”でした」というオチになるのですが、何とこの問題には数学的にもチャンとした解が存在するのです(ビックリ!)。
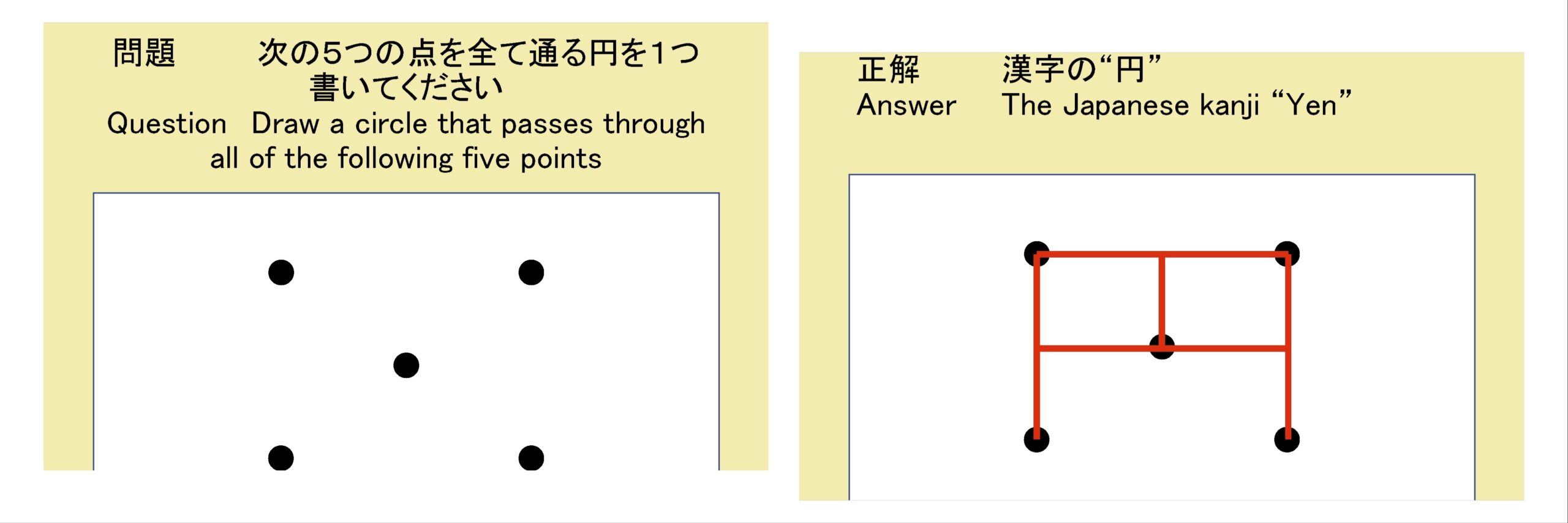
文中の“5つの点”というところが、実は(数学としても)なかなか理に適っていて、一般の2次曲線を表す方程式は
x 2 + A x y + B y 2 + C x + D y + E = 0
という5つの未定係数を含むもの、つまり元から(ただし複素空間内の)5つの点を通っているというワケです。これら5つの点を、例えば
(0, 0), (1, ±1), (-1, ±√3 i )
として連立方程式を解くと
A = 0, B = 1, C = -2, D = 0, E = 0
となって、円の方程式
(x – 1) 2 + y 2 = 1
が得られるのですが……あれっ?
だとすると、通常の円は3点を通る(同一直線上にない3点で決まる)というのが、中学数学からの“言わずもがなの常識”なんですけど、5点を通るとなると、残りの2点は一体どこにあるのでしょうか?
話がここまでくると、ユークリッド平面 E 2 = {(x, y ) | x, y ∈ R } の代わりに複素射影平面 CP 2 = {(X, Y, Z ), x = X / Z, y = Y / Z | X, Y, Z ∈ C } を考えてやらなければダメで、円の方程式がこの射影座標(または同次座標とも)では
(X / Z ) 2 + (Y / Z ) 2 = 1(つまり X 2 + Y 2 = Z 2)
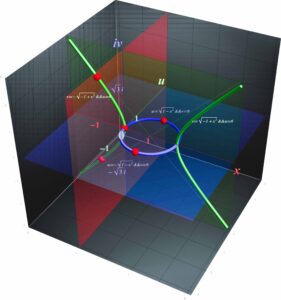
と表されることから、“全ての円”は無限遠直線 Z = 0 上にある2つの“虚円点 (circular points at infinity または isotropic points)” (1, ±i , 0) ※を“常に”通っていたのでした。
※上式 X 2 + Y 2 = Z 2 で Z = 0 と置いた X 2 + Y 2 = 0 を解いて得られる。
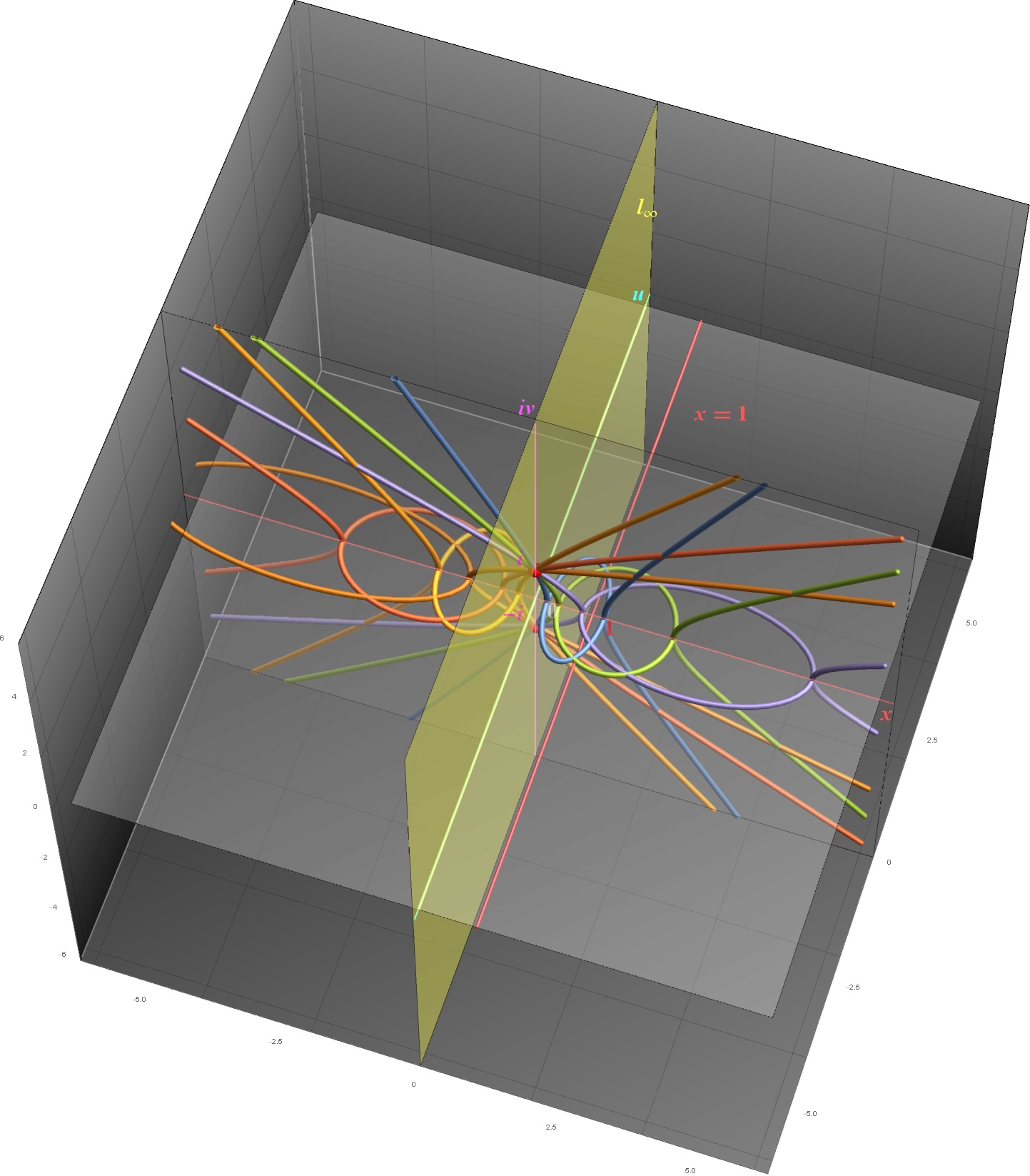
虚円点の概念は、射影幾何学を近代に復活させたフランスの数学者ジャン=ヴィクトル・ポンスレ (1788-1867) によって導入されました。信じられないかもしれませんが、虚円点は幾何学に関する数多くの本で紹介されていますが、これらの複素かつ無限遠領域における振る舞いが正しくレンダリングされたことは、これまでに一度もありませんでした。
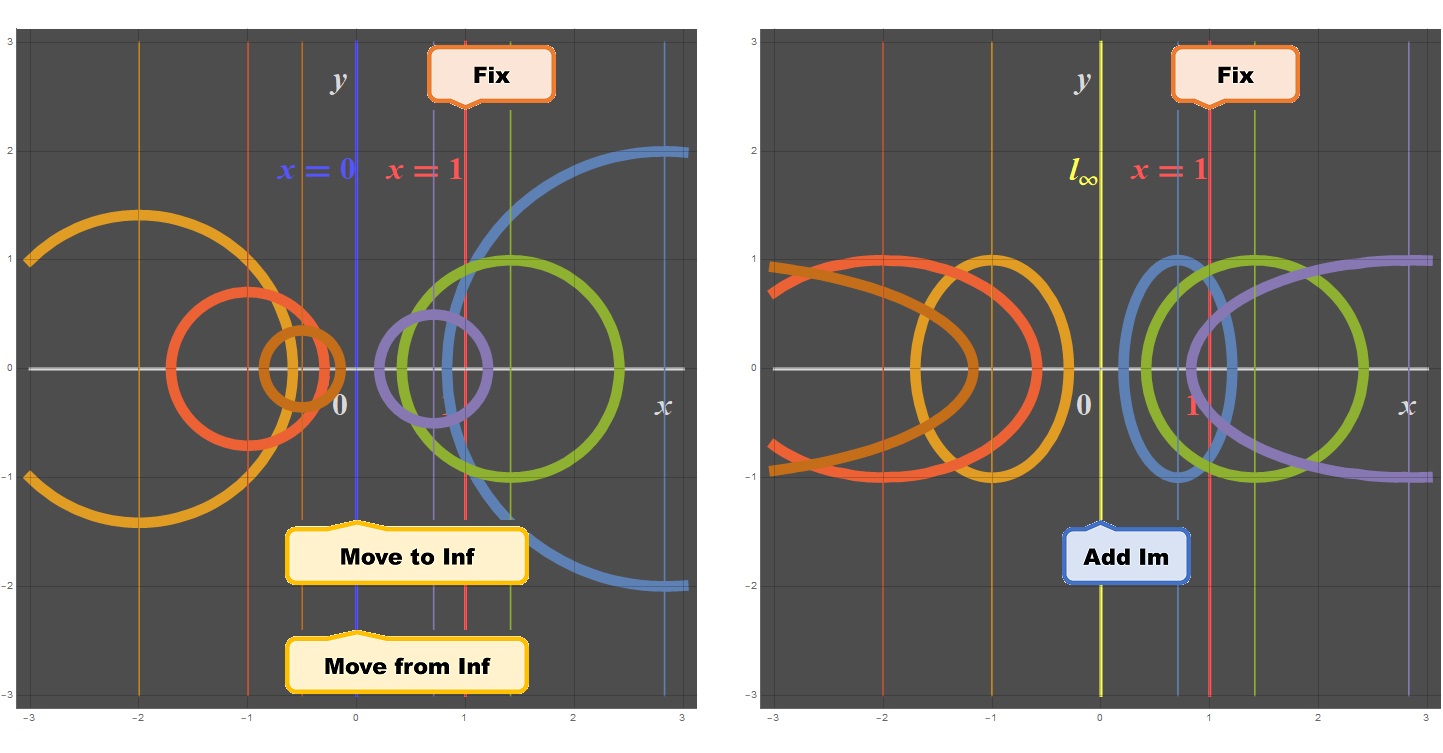
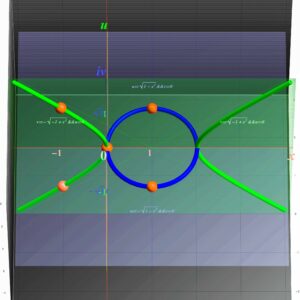
有限の直線 x = 1 を固定しながら無限遠直線を直線 x = 0 まで平行移動し、それを実数から複素数へ拡張することにより、2つの虚円点(赤い点)を確認することができます。
私たちは、ユーザーが3次元ユークリッド空間 E 3 を超えて環境の境界を設定できる没入型仮想環境を研究しています。より具体的には、その境界をn 次元の複素射影空間 CP n へ拡張することにより、ユークリッド空間で認識可能な形式として、複素領域と無限遠領域の両方の要素を自然に可視化することができます。ここでの問題は、数学のレベルが高くなればなるほど、高度な学位を持つ専門家だけが理解できるように、可視化方法が抽象的になる傾向があることです。初歩的な数学的可視化とより高度な数学的可視化の間のギャップを埋めるために、引き続き、私たちの具象的なアプローチがどのように不可欠であるかを示していきます。
メンバ
藤代研究室に所属しているメンバは名前の前に藤代研のアイコン![]() がついています。
がついています。
| 名前 | 現在の所属 | ホームページ |
|---|---|---|
| 慶應義塾大学 |
ビデオ
業績
論文誌
会議・シンポジウム
国際会議・シンポジウム
国内会議・シンポジウム
発表
資金